ChatGPT kann nicht rechnen!

GPT steht für „Generative Pre-trained Transformer“ und ist ein künstlicher Intelligenz-Textgenerator, der auf der Grundlage von statistischen Verfahren und Mustern aus großen Textkorpora trainiert wird. GPT-Modelle lernen, Texte zu generieren, indem sie die Wahrscheinlichkeiten der Wörter oder Wortfolgen in einem bestimmten Kontext schätzen. Im Wesentlichen handelt es sich um ein komplexes statistisches Modell, das auf die Vorhersage von Textsequenzen abzielt. (das hatte ich im Artikel Generative Pre-trained Transformer (GPT): Ein plappernder stochastischer Papagei genauer erklärt)

Wir brechen das an einem Beispiel runter

Da das GPT-Modell keine spezielle Mathematik- oder Rechenlogik implementiert, ist es nicht in der Lage, mathematische Probleme wie ein traditioneller Rechenalgorithmus zu lösen. Stattdessen verlässt es sich auf die in den Trainingsdaten identifizierten Muster und Wahrscheinlichkeiten, um mathematische Aufgaben zu bewältigen. In vielen Fällen kann das GPT-Modell einfache Rechenaufgaben richtig lösen, weil es genügend Beispiele in den Trainingsdaten gesehen hat. Für komplexere oder weniger häufige Rechenprobleme könnte das GPT-Modell jedoch Schwierigkeiten haben, eine korrekte Lösung zu finden oder es lügt Dir einfach eine komplett falsche Lösung vor!

6+3

Stellen wir uns vor, wir haben eine einfache Rechenoperation wie „6 + 3“ und möchten, dass ein GPT-Modell diese Aufgabe löst.

Da das GPT-Modell während des Trainings viele Texte gesehen hat, in denen einfache Additionen vorkommen, ist es wahrscheinlich, dass das Modell die korrekte Antwort „9“ liefert. Dies liegt daran, dass es aus den Trainingsdaten gelernt hat, dass in vielen Kontexten, in denen die Zahlen „6“ und „3“ sowie das Pluszeichen auftauchen, die korrekte Antwort „9“ ist.

9.465.748+234.235

Wenn ein GPT-Modell auf eine Rechenaufgabe wie „9465748 + 234235“ stößt, die es in den Trainingsdaten noch nie gesehen hat, kann es dennoch versuchen, eine Antwort darauf zu geben. Dabei stützt es sich auf das erlernte Wissen aus ähnlichen Mustern und Kontexten, die es in den Trainingsdaten gesehen hat.

In diesem Fall könnte das GPT-Modell versuchen, die Aufgabe basierend auf seinem Verständnis von Addition und der Positionierung von Zahlen zu lösen. Das Modell hat möglicherweise gelernt, wie es große Zahlen addieren kann, indem es die Zahlen in den verschiedenen Stellen (Einheiten, Zehner, Hunderter usw.) kombiniert. Es könnte versuchen, die Zahlen in der Rechenaufgabe auf diese Weise zu addieren, um eine Antwort zu erhalten.

Da das Modell auf der Grundlage von statistischen Mustern und Wahrscheinlichkeiten arbeitet, besteht die Möglichkeit, dass es eine falsche Antwort gibt, wenn es keine ausreichend ähnlichen Beispiele in den Trainingsdaten gesehen hat.

Warum es nicht hilf, ChatGPT nach dem Lösungsweg zu fragen

Hier kommt wieder der stochastische Papagei zum tragen. Bei wirklich leichten Operationen kann ChatGPT das aus vielen Trainingsdaten ableiten und weiß, dass man beiden Zahlen spaltenweise von rechts nach links addiert (unter Berücksichtigung eventueller Überhänge).

ChatGPT würde das so beschreiben:

1. Zerlege die beiden Zahlen in ihre einzelnen Ziffern: 9, 4, 6, 5, 7, 4, 8 und 2, 3, 4, 2, 3, 5.

2. Addiere die Ziffern paarweise von rechts nach links und berücksichtige Übertragungen, wenn die Summe einer Ziffernpaarung 10 oder mehr beträgt.

8 + 5 = 13 → Schreibe die 3 und merke den Übertrag von 1.
4 (mit Übertrag 1) + 4 + 3 = 8 → Schreibe die 8.
7 + 2 + 2 = 11 → Schreibe die 1 und merke den Übertrag von 1.
5 (mit Übertrag 1) + 3 = 9 → Schreibe die 9.
6 + 4 = 10 → Schreibe die 0 und merke den Übertrag von 1.
4 (mit Übertrag 1) + 3 = 6 → Schreibe die 6.
9 + 2 = 9 → Schreibe die 9.

Kombiniere die erhaltenen Ziffern von links nach rechts: 9699983.

Oder so:

  9465748
+  234235
_________
  9699983

Beides richtig. Aber jedes mal eine Andere Erklärung, auf die selbe Frage: „Gib mit den Lösungsweg“. Hier spielt vor allem der Kontext vorher eine Rolle. In der ersten Antwort habe ich ChatGPT aufgefordert, sich so zu verhalten, wie das ein Lehrer in der Schule machen würde. Im Zweiten Beispiel gab es gar keinen Kontext.

Wer sich näher mit der Auswirkung von Kontext bei ChatGPT auseinandersetzen will, dem empfehle ich ein kleines Spiel:

https://gpa.43z.one/?ref=producthunt

Implizites Verständnis, Kontext und Muster über mathematische Operationen

ChatGPT hat durch die vielen Trainingsdaten also eine Idee, was eine Kolonnenaddition (oder „Addition im Stellenwertsystem“) ist und kann diese (entlang seiner Muster) anwenden. Das geht sehr oft gut, aber auch sehr oft schief! Vor allem, wenn man einen Lösungsweg braucht (Liebe Schüler, passt da echt auf!).

Wer das alles sehr ausführlich sehen will, schaut bei Edmund Weitz (Mathematiker, Informatiker und Professor an der Hochschule für Angewandte Wissenschaften Hamburg (HAW Hamburg)) vorbei:

Wie macht ChatGPT das nun?

Ab hier wird es kompliziert und wir steigen Tief in das Thema Token und Vektoren ein. Ich versuche es trotzdem anschaulich und leicht verständlich zu halten.

Wir konstruieren uns ein Beispiel. ChatGPT greift auf Wahrscheinlichkeiten und Muster in den Textdaten zu, die es während des Trainings gesehen hat.

Ein GPT-Modell kann jedoch bestimmte Muster oder Wahrscheinlichkeiten in Bezug auf mathematische Operationen lernen. Hier ist eine hypothetische Tabelle, die die Häufigkeit von bestimmten Rechenoperationen und ihren Ergebnissen in den Trainingsdaten des Modells darstellt:

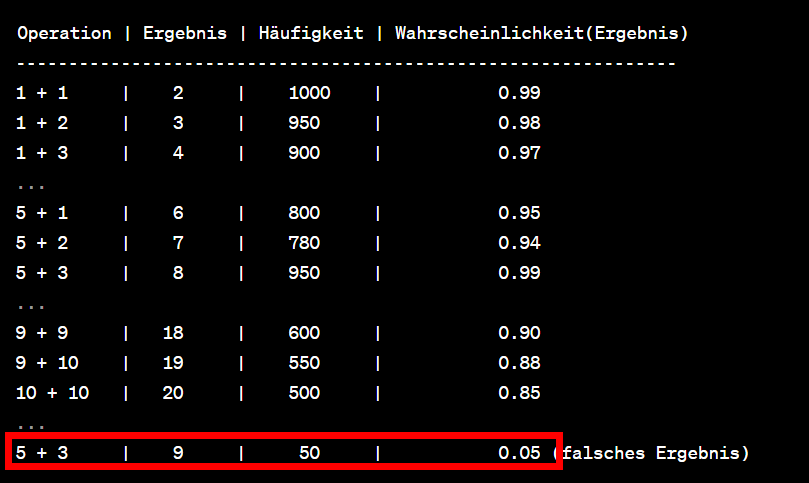
In dieser Tabelle repräsentiert die Spalte „Ergebnis“ das Ergebnis jeder Rechenoperation. Die Spalte „Wahrscheinlichkeit(Ergebnis)“ zeigt die Wahrscheinlichkeit, dass das Ergebnis der jeweiligen Rechenoperation korrekt ist, basierend auf den Mustern in den Trainingsdaten.

Achtung: Diese Beispiel ist sehr stark vereinfacht. GPT-Modelle basieren auf komplexen neuronalen Netzwerkstrukturen, um die Zusammenhänge zwischen Wörtern und Phrasen in den Textdaten zu erfassen und darauf basierend Vorhersagen zu treffen. In der Praxis wäre die Berechnung der Wahrscheinlichkeit für ein bestimmtes Ergebnis aufgrund der Vielzahl der Faktoren, die das Modell berücksichtigt, wesentlich komplexer (und nicht mehr gut darstellbar).

Was passiert, wenn eine Lösung nicht schon statistisch vorhanden ist?

Ein GPT-Modell (Generative Pre-trained Transformer) ist ein auf maschinellem Lernen basierendes Sprachmodell, das Text basierend auf statistischen Mustern generiert, die es in seinen Trainingsdaten gelernt hat. Obwohl es kein explizites Verständnis von mathematischen Operationen hat, kann es dennoch ein gewisses Maß an „allgemeinem Verständnis“ entwickeln, indem es Muster und Zusammenhänge in den Trainingsdaten erkennt.

Ein GPT-Modell ist so konzipiert, dass es den Kontext von Wörtern und Phrasen in einer Textsequenz berücksichtigt und basierend auf diesem Kontext die Wahrscheinlichkeit des nächsten Wortes oder der nächsten Phrase vorhersagt. Während des Trainings lernt das Modell, diese Vorhersagen durch Analyse von Millionen von Textbeispielen zu treffen, die verschiedene Themen und Inhalte abdecken, einschließlich mathematischer Operationen und Begriffe.

Wenn das GPT-Modell in seinen Trainingsdaten ausreichend Beispiele für mathematische Operationen und Zusammenhänge sieht, kann es beginnen, ein allgemeines Verständnis dafür zu entwickeln, wie diese Operationen funktionieren und wie sie sich aufeinander beziehen. Das bedeutet, dass es in der Lage sein kann, bestimmte Arten von mathematischen Problemen zu lösen, auch wenn es kein explizites Verständnis der zugrunde liegenden mathematischen Regeln hat.

Dieses allgemeine Verständnis ist jedoch begrenzt und kann in manchen Fällen ungenau oder unzuverlässig sein. Da das GPT-Modell auf statistischen Mustern basiert und nicht auf festen Regeln oder Logik, kann es Schwierigkeiten haben, mathematische Probleme zu lösen, die über die Muster hinausgehen, die es in seinen Trainingsdaten gesehen hat. Das Modell kann auch inkonsistente oder widersprüchliche Informationen aus den Trainingsdaten übernehmen, was zu falschen Vorhersagen führen kann.

Insgesamt ist das „allgemeine Verständnis“ eines GPT-Modells für mathematische Operationen eher ein Nebenprodukt seiner Fähigkeit, Muster und Zusammenhänge in Textdaten zu erkennen, als ein explizites Verständnis von Mathematik oder Rechenregeln.

Kleiner Ausflug in die Vektoren

Für alle, die aus der Suchmaschinenoptimierung kommen, klingelt es bei Multidimensionalen Vektoren. Ja, ich meine Word2Vec. Wir beschäftigen uns als SEO also schon seit knapp 10 Jahren mit statistischen Modellen, die in der Lage sind erstaunliche Ergebnisse zu erzielen. Ein word2vec Model, welches mit Wikipedia trainiert ist, konnte schon 2013 Fragen beantworten. Das hat nur niemand in der Öffentlichkeit mitbekommen. Erst ChatGPT hat diesen Sprung gemacht.

Word2Vec ist ein Verfahren, das Wörter in einem Text in Vektoren konvertiert, sodass ähnliche Wörter im Vektorraum nahe beieinander liegen. Es basiert auf zwei Hauptarchitekturen: dem Continuous Bag-of-Words-Modell (CBOW) und dem Skip-Gram-Modell. Word2Vec verwendet die räumliche Nähe der Vektoren, um die semantische Ähnlichkeit zwischen Wörtern zu erfassen. Es handelt sich um ein unsupervised Learning-Verfahren, das auf der Beobachtung von Wörtern in ihrem Kontext in großen Textkorpora basiert.

GPT-Modelle hingegen sind auf der Transformer-Architektur aufgebaut, einer speziellen Art von neuronalen Netzwerken, die für die Verarbeitung von Sequenzdaten entwickelt wurden. GPT-Modelle lernen sowohl die semantischen als auch die syntaktischen Beziehungen zwischen Wörtern und Phrasen in den Trainingsdaten.

Der wirklich wichtige Unterschied ist aber:

Im Gegensatz zu Word2Vec, das hauptsächlich darauf abzielt, Wörter in einem Vektorraum darzustellen, zielen GPT-Modelle darauf ab, Text basierend auf der vorherigen Textsequenz zu generieren.

Die Ähnlichkeit zwischen beiden Verfahren liegt darin, dass sie beide auf der Analyse von Textkorpora basieren und versuchen, Muster und Zusammenhänge in den Daten zu erkennen. Beide Verfahren verwenden Vektorrepräsentationen von Wörtern, um ihre Beziehungen zueinander zu modellieren. In Bezug auf die Statistik könnten beide Verfahren als statistische Modelle betrachtet werden, da sie auf der Analyse von Häufigkeiten und Mustern in großen Textkorpora basieren.

Wer sich also mit Word2Vec beschäftigt hat, hat ein kleinen Verständnisvorsprung. 😉

Jetzt schauen wir, wie GPT die Aufgabe wirklich löst!

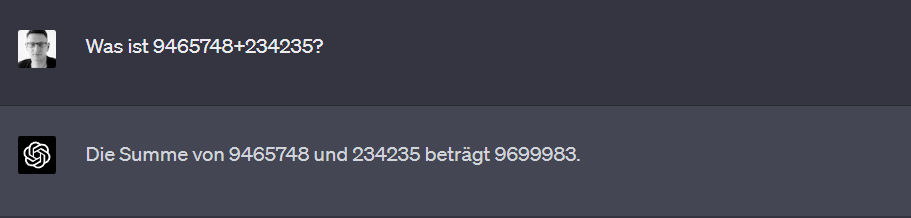
Um zu verdeutlichen, wie ein GPT-Modell mit der Frage „Was ist 9465748+234235?“ umgehen würde, betrachten wir die grundlegenden Mechanismen, die das Modell verwendet, um Vorhersagen zu treffen.

1. Tokenisierung: Zuerst wird die Eingabe, in diesem Fall die Frage „Was ist 9465748+234235?“, in eine Sequenz von Token (Wörter oder Zeichen) zerlegt. Das GPT-Modell verwendet diese Token als Eingabe, um die Aufgabe zu lösen.
2. Kontextverständnis: Das GPT-Modell analysiert die Eingabesequenz und versucht, den Kontext und die Bedeutung der einzelnen Token zu verstehen. In diesem Fall erkennt es, dass es sich bei der Eingabe um eine Rechenaufgabe handelt, nämlich eine Addition.
3. Textgenerierung: Basierend auf dem Kontext und der Bedeutung der Eingabe, versucht das GPT-Modell, die wahrscheinlichste Antwort auf die Frage vorherzusagen. Es generiert dabei Text, der auf den statistischen Mustern basiert, die es in den Trainingsdaten gelernt hat.
4. Antwort: Das GPT-Modell generiert eine Antwort, indem es die Wahrscheinlichkeiten der möglichen Ergebnisse basierend auf den gelernten Mustern bewertet. In diesem Fall würde das Modell vermutlich korrekt vorhersagen, dass das Ergebnis der Addition 9465748+234235 gleich 9699983 ist.

Die Tokenisierung der Anfrage „Was ist 9465748+234235?“ hängt von der spezifischen Tokenisierungsmethode ab, die das GPT-Modell verwendet. Generell gibt es zwei Hauptansätze für die Tokenisierung: die auf Wortebene und die auf Subworte-Ebene. Im Fall von GPT-Modellen wird häufig die Subworte-Tokenisierung (Byte Pair Encoding, BPE) verwendet, die sowohl für die Englishe als auch für die Deutsche Sprache gut funktioniert.

Angenommen, wir verwenden eine Subworte-Tokenisierung für das GPT-Modell, könnte die Tokenisierung der Anfrage „Was ist 9465748+234235?“ etwa so aussehen:

["Was", " ist", " ", "946", "574", "8", "+", "234", "235"]

In diesem Beispiel wurde die Anfrage in einzelne Subworte und Zeichen aufgeteilt. Die genaue Tokenisierung kann jedoch je nach Implementierung und verwendeten Vokabular variieren.

Sobald die Eingabe in Token zerlegt ist, verarbeitet das GPT-Modell die Sequenz, um den Kontext und die Bedeutung der einzelnen Token zu erfassen und eine Vorhersage für das Ergebnis der Rechenaufgabe zu treffen.

In einem GPT-Modell erfolgt die Verarbeitung der Token mithilfe der Transformer-Architektur, die auf selbst-attentiven Mechanismen basiert. Der Kontext kommt aus der Position der Token innerhalb der Eingabesequenz und den Beziehungen zwischen den Token.

Hier ist ein vereinfachtes Beispiel, wie das GPT-Modell die Eingabe „Was ist 9465748+234235?“ verarbeitet:

• Token-Vektoren: Jedes Token in der Eingabesequenz wird in einen Vektor umgewandelt, der seine Bedeutung repräsentiert. Diese Vektoren werden durch ein Einbettungsverfahren erstellt, das auf den Trainingsdaten des Modells basiert.
• Positionsinformation: Da die Reihenfolge der Token in der Eingabe wichtig ist, fügt das GPT-Modell Positionsinformationen zu den Token-Vektoren hinzu. Dies ermöglicht es dem Modell, die Beziehungen zwischen den Token in der Sequenz zu erkennen.
• Selbst-Attention-Mechanismus: Der Transformer verwendet den Selbst-Attention-Mechanismus, um die Beziehungen zwischen den Token in der Eingabesequenz zu analysieren. Die Idee besteht darin, jedes Token in Bezug auf alle anderen Token in der Sequenz zu „bewerten“, um zu bestimmen, wie wichtig die Beziehung zwischen den Token ist. Diese Bewertungen werden dann verwendet, um eine gewichtete Summe der Eingabe-Token-Vektoren zu berechnen.
• Feed-Forward-Netzwerke und Layer-Normalisierung: Nachdem die selbst-attentiven Gewichtungen berechnet wurden, werden die Token-Vektoren durch Feed-Forward-Netzwerke und Layer-Normalisierung weiter verarbeitet. Dies sind Standardverfahren in neuronalen Netzwerken, die zur Transformation und Stabilisierung der Vektorrepräsentationen beitragen.
• Textgenerierung: Am Ende der Verarbeitung erstellt das GPT-Modell eine Vorhersage für das nächste Token in der Sequenz basierend auf den verarbeiteten Token-Vektoren. Im Fall der Rechenaufgabe „Was ist 9465748+234235?“ würde das Modell versuchen, die wahrscheinlichste Antwort als nächstes Token vorherzusagen.

Die wahrscheinlichste Antwort kommt aus der Analyse der Token und deren Beziehungen zueinander, die das GPT-Modell während des Trainings gelernt hat. Das Modell lernt, wie verschiedene Token in den Trainingsdaten zusammenhängen, und verwendet diese Informationen, um Vorhersagen für das nächste Token in der Sequenz zu treffen.

Im Fall der Rechenaufgabe „Was ist 9465748+234235?“ hat das Modell während des Trainings viele Beispiele von Rechenaufgaben gesehen und die zugrunde liegenden Muster und Strukturen gelernt. Basierend auf diesen Mustern und den Beziehungen zwischen den Token in der Eingabesequenz kann das GPT-Modell die wahrscheinlichste Antwort vorhersagen.

Nach der Verarbeitung dieser Token könnte das Modell die folgenden möglichen Antworten generieren, die jeweils mit einer Wahrscheinlichkeit verbunden sind:

{
  "9": 0.002,
  "6": 0.001,
  "9": 0.002,
  ...
  "9699983": 0.85,
  ...
  "12345": 0.001
}

In diesem hypothetischen Beispiel wäre die wahrscheinlichste Antwort „9699983“ mit einer Wahrscheinlichkeit von 0,85. Das GPT-Modell würde dann diese Antwort als nächstes Token in der Sequenz auswählen.

In unserem hypothetischem Model sieht man also, dass die Antwort nicht mit eine Wahrscheinlichkeit von 100% gegeben wird, sondern nur 85%. In einem realistischen Szenario ist die Wahrscheinlichkeit eher 99,999910113372342%. 😀

Fazit

Wieder so ein langer Artikel den niemand liest. Vor allem nicht die Leute, die behaupten, dass ChatGPT denken kann. Oder Wörter für die Ausgabe zählen oder eben rechnen.

tldr;

Nein. ChatGPT kann nicht rechnen. Dafür rechnet es aber ziemlich gut!